某种电子元件的重量x(单位:g)服从正态分布,μ,σ2均未知。测得16只元件的重量如下:159,280,101,212,
A.提出假设:H0:μ≤225;H1:μ>225
B.提出假设:H0:μ≥225;H1:μ<225
C.检验统计量及其概率分布为1.jpg)
D.取α=0.05,经计算有:T<t0.05(15)
E.接受H0,即认为元件的平均重量不大于225g
 如搜索结果不匹配,请 联系老师 获取答案
如搜索结果不匹配,请 联系老师 获取答案
A.提出假设:H0:μ≤225;H1:μ>225
B.提出假设:H0:μ≥225;H1:μ<225
C.检验统计量及其概率分布为1.jpg)
D.取α=0.05,经计算有:T<t0.05(15)
E.接受H0,即认为元件的平均重量不大于225g
 如搜索结果不匹配,请 联系老师 获取答案
如搜索结果不匹配,请 联系老师 获取答案
 更多“某种电子元件的重量x(单位:g)服从正态分布,μ,σ2均未知…”相关的问题
更多“某种电子元件的重量x(单位:g)服从正态分布,μ,σ2均未知…”相关的问题
第1题
某种电子元件的寿命x(单位:小时)服从正态分布。现测得16只元件的寿命如下:
159 280 101 212 224 379 179 264
222 362 168 250 149 260 485 170
问是否有理由认为元件的平均寿命显著地大于225小时(a=0.05)?
第2题
其体重为

(1)试估计新生男婴平均体重的95%置信区间;(2)试估计新生男婴体重方差的90%置信区间.
解题提示正态总体方差的区间估计用X2分布进行计算.
第3题
第4题
从一批零件中,随机抽取9个,测得其重量(g)为
312 313 3.9 310 311 314 315 308 307
设零件重量服从正态分布,求零件重量的数学期望对应于置信水平0.95的置信区间.
第6题
已知某种电子元件的使用寿命X(h)服从指数分布e(λ)。抽查100个元件,得样本均值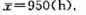 。能否认为参数λ=0.001(a=0.05)?
。能否认为参数λ=0.001(a=0.05)?
第7题
已知某种电子元件的使用寿命X(h)服从指数分布e(λ),抽查100个元件,得样本均值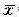 =950(h)。能否认为参数λ=0.001(α=0.05)?
=950(h)。能否认为参数λ=0.001(α=0.05)?
第9题
A.e- 1.5+e-3
B.e- 1.5-e-3
C.-e- 1.5+e-3
D.e 1.5-e-3
第10题
源电压X服从正态分布N(220,252),试求
(1) 该电子元件损坏的概率α;
(2) 该电子元件损坏时,电源电压在200~240V的概率β.


为了保护您的账号安全,请在“赏学吧”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!

 微信搜一搜
微信搜一搜
 赏学吧
赏学吧



 微信搜一搜
微信搜一搜
 赏学吧
赏学吧