题目内容
(请给出正确答案)
[主观题]
设< G,*>是一个群,证明:如果对任意的a,b∈G都有是一个阿贝尔群。
设< G,*>是一个群,证明:如果对任意的a,b∈G都有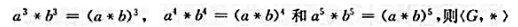 是一个阿贝尔群。
是一个阿贝尔群。
 如搜索结果不匹配,请 联系老师 获取答案
如搜索结果不匹配,请 联系老师 获取答案
设< G,*>是一个群,证明:如果对任意的a,b∈G都有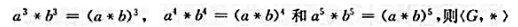 是一个阿贝尔群。
是一个阿贝尔群。
 如搜索结果不匹配,请 联系老师 获取答案
如搜索结果不匹配,请 联系老师 获取答案
 更多“设< G,*>是一个群,证明:如果对任意的a,b∈G都有是一…”相关的问题
更多“设< G,*>是一个群,证明:如果对任意的a,b∈G都有是一…”相关的问题
第1题
设(G,*)是群,如果对于群G中任意元素a、b都有(a*b)-1=a-1*b-1,证明(G,*)是阿贝尔群。
第3题
设(G,*)是一个独异点,并且对于G中的每一个元素x都有x*x=e,其中e是单位元.证明:(G,*)是一个阿贝尔群.
第5题
设f1、f2都是从代数系统(A,★)到(B,*)的同态.设g是从A到B的一个映射,使得对任意a∈A都有g(a)=f1(a)*f2(a).证明:如果(B,*)是一个可交换半群,那么g是由(A,★)到(B,*)的同态.
第6题
设u是群(G,)中给定的一个元素,其逆元素为u-1,对G定义一个新的运算“*”:对任意a,b∈G,
.试证明(G,*)也是一个群。
第7题
设u是群(G,+)中取定的一个元素,其逆元素为u-1,对G定义运算*为:对任意a,b∈G,a*b=a*u-1*b,试证明(G,*)也是一个群.
第8题
设(G,*)是一个群,对于任意的a∈G,令H={y|y*a=a*y,y∈G},证明(H,*)是(G,*)的子群.
第9题
设(G,△)是一个群,而a∈G.如果f是从G到G的映射,使得对于每一个x∈G,都有f(x)=a△x△a-1,证明:f是从G到G的自同构.
第11题
设(H,*)是群(G,*)的子群,如果A={x|x∈G,x*H*x-1=H},证明(A,*)是(G,*)的一个子群.


为了保护您的账号安全,请在“赏学吧”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!

 微信搜一搜
微信搜一搜
 赏学吧
赏学吧



 微信搜一搜
微信搜一搜
 赏学吧
赏学吧